Distances dans l’espace

La distance entre la Terre et la Lune est énorme, mais elle semble minuscule par rapport à l’échelle de l’espace.

On sait que l’espace est très grand, c’est pourquoi les astronomes n’utilisent pas le système métrique auquel nous sommes habitués pour le mesurer. Dans le cas de la distance à la Lune (384 000 km), les kilomètres peuvent encore s’appliquer, mais si nous exprimons la distance à Pluton dans ces unités, nous obtenons 4 250 000 000 km, ce qui est moins pratique pour l’enregistrement et les calculs. C’est pourquoi les astronomes utilisent d’autres unités de mesure de la distance, que vous pouvez découvrir ci-dessous.

Unité astronomique

La plus petite de ces unités est l’unité astronomique (u.a.). Historiquement, une unité astronomique équivaut au rayon de l’orbite de la Terre autour du Soleil, soit la distance moyenne entre la surface de notre planète et le Soleil. Cette méthode de mesure était la plus appropriée pour étudier la structure du système solaire au XVIIe siècle. Sa valeur exacte est de 149 597 870 700 mètres. Aujourd’hui, l’unité astronomique est utilisée dans les calculs portant sur des longueurs relativement faibles. C’est-à-dire dans l’étude des distances à l’intérieur du système solaire ou d’autres systèmes planétaires.

Année-lumière

L’année-lumière est une unité de longueur un peu plus grande en astronomie. Elle correspond à la distance parcourue par la lumière dans le vide en une année terrestre julienne. Elle implique également une influence nulle des forces gravitationnelles sur sa trajectoire. Une année-lumière représente environ 9 460 730 472 580 km ou 63 241 u.a. Cette unité de longueur n’est utilisée que dans la littérature scientifique de vulgarisation, car l’année-lumière permet au lecteur de se faire une idée approximative des distances à l’échelle galactique. Toutefois, en raison de son imprécision et de son inconvénient, l’année-lumière n’est pratiquement pas utilisée dans les travaux scientifiques.

Matériel par thème

Parsec

L’unité de mesure de distance la plus pratique et la plus commode pour les calculs astronomiques est le parsec. Pour comprendre sa signification physique, il est nécessaire de considérer le phénomène de parallaxe. En substance, lorsqu’un observateur se déplace par rapport à deux corps éloignés, la distance apparente entre ces corps change également. Dans le cas des étoiles, le phénomène suivant se produit. Lorsque la Terre se déplace sur son orbite autour du Soleil, la position visuelle des étoiles proches de nous change légèrement, tandis que les étoiles lointaines, qui servent d’arrière-plan, restent à la même place. Le changement de position d’une étoile lorsque la Terre se déplace d’un rayon de son orbite s’appelle la parallaxe annuelle, qui se mesure en secondes angulaires

Un parsec est donc égal à la distance d’une étoile dont la parallaxe annuelle est égale à une seconde angulaire, une unité de mesure d’angle en astronomie. D’où le nom de «parsec», issu de deux mots : «parallaxe» et «seconde». La valeur exacte d’un parsec est de 3,0856776-10 16 mètres ou 3,2616 années-lumière. 1 parsec est égal à environ 206 264,8 a.u.

Méthode de localisation par laser et radiolocalisation

Ces deux méthodes modernes permettent de déterminer la distance exacte d’un objet dans le système solaire. Elles se déroulent de la manière suivante. À l’aide d’un puissant émetteur radio, un signal radio directionnel est envoyé vers l’objet observé. Celui-ci bat alors le signal reçu et le renvoie vers la Terre. Le temps mis par le signal pour parcourir le trajet détermine la distance qui le sépare de l’objet. La précision de la radiolocalisation n’est que de quelques kilomètres. Dans le cas de la localisation par laser, au lieu d’un signal radio, le laser envoie un faisceau lumineux qui permet des calculs similaires pour déterminer la distance par rapport à l’objet. La précision de la localisation laser est de l’ordre de la fraction de centimètre.

Télescope TG-1 du localisateur laser LE-1, site d’essai de Sary-Shagan.

Méthode trigonométrique de la parallaxe

La méthode la plus simple pour mesurer la distance d’objets spatiaux éloignés est la méthode trigonométrique de la parallaxe. Elle est basée sur la géométrie scolaire et consiste en ce qui suit. Nous traçons un segment (ligne de base) entre deux points de la surface de la Terre. Choisissons un objet dans le ciel, dont nous voulons mesurer la distance, et définissons-le comme sommet du triangle obtenu. Nous mesurons ensuite les angles entre la base et les lignes tracées à partir des points choisis jusqu’au corps dans le ciel. Connaissant le côté et les deux angles adjacents du triangle, nous pouvons trouver tous ses autres éléments.

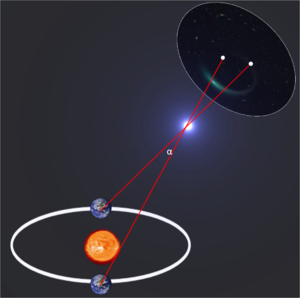
La valeur de la ligne de base choisie détermine la précision de la mesure. En effet, si l’étoile est située à une très grande distance de nous, les angles mesurés seront presque perpendiculaires à la ligne de base et l’erreur dans leur mesure peut affecter de manière significative la précision de la distance calculée par rapport à l’objet. Il est donc nécessaire de choisir les points les plus éloignés de la Terre comme ligne de base. Initialement, le rayon de la Terre servait de ligne de base. En d’autres termes, des observateurs étaient placés en différents points du globe et mesuraient les angles mentionnés, et l’angle opposé à la ligne de base était appelé parallaxe horizontale. Plus tard, cependant, une distance plus grande — le rayon moyen de l’orbite terrestre (une unité astronomique) — a été prise comme ligne de base, ce qui a permis de mesurer la distance d’objets plus éloignés. Dans ce cas, l’angle opposé à la ligne de base est appelé parallaxe annuelle.

Cette méthode n’est pas très pratique pour la recherche à partir de la Terre car, en raison des interférences de l’atmosphère terrestre, il n’est pas possible de déterminer la parallaxe annuelle d’objets situés à plus de 100 parsecs.

Cependant, en 1989, l’Agence spatiale européenne a lancé le télescope spatial Hipparcos, qui a permis d’identifier des étoiles à une distance allant jusqu’à 1 000 parsecs. Grâce aux données obtenues, les scientifiques ont pu établir une carte tridimensionnelle de la répartition de ces étoiles autour du Soleil. En 2013, l’ESA a lancé le satellite suivant, Gaia, dont la précision de mesure est 100 fois supérieure, permettant d’observer toutes les étoiles de la Voie lactée. Si les yeux humains avaient la précision du télescope Gaia, nous pourrions voir le diamètre d’un cheveu humain à une distance de 2 000 kilomètres.

La méthode de la bougie standard

La méthode de la bougie standard est utilisée pour déterminer les distances des étoiles dans d’autres galaxies et les distances de ces galaxies elles-mêmes. Comme nous le savons, plus la source lumineuse est éloignée de l’observateur, plus elle lui apparaît faible. Par exemple, l’éclairage d’une ampoule à une distance de 2 mètres sera 4 fois plus faible qu’à une distance de 1 mètre. C’est le principe selon lequel la distance aux objets est mesurée par la méthode de la bougie standard. Ainsi, en faisant l’analogie entre une ampoule et une étoile, on peut comparer les distances à des sources lumineuses de puissances connues.

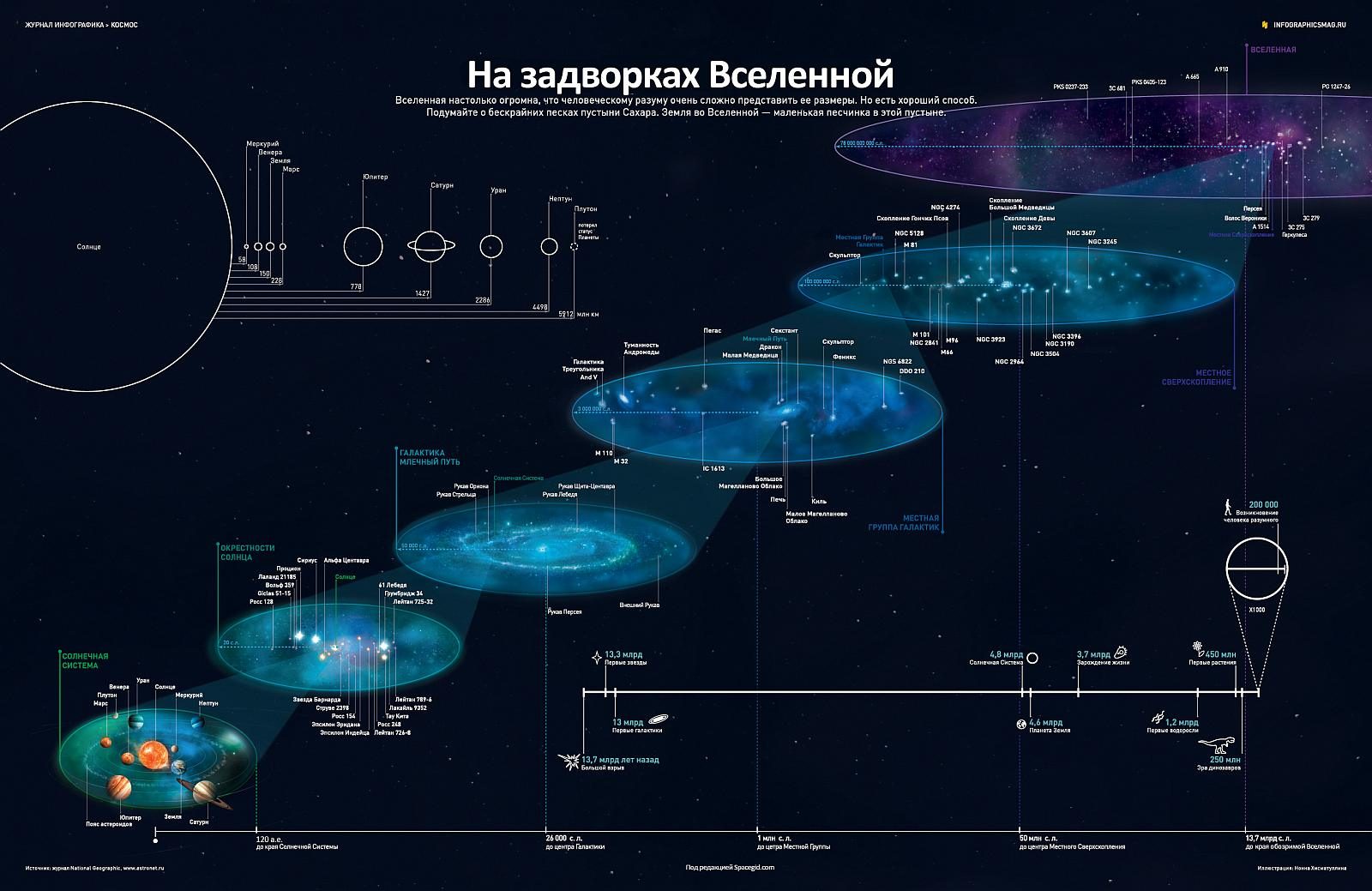
L’échelle de l’Univers explorée par les méthodes existantes est impressionnante. Voir l’infographie en taille réelle.

Les bougies standard en astronomie sont des objets dont la luminosité (analogue de la puissance de la source) est connue. Il peut s’agir de n’importe quel type d’étoile. Pour déterminer sa luminosité, les astronomes mesurent la température de sa surface en fonction de la fréquence de son rayonnement électromagnétique. Puis, connaissant la température, qui permet de déterminer la classe spectrale de l’étoile, ils déterminent sa luminosité à l’aide du diagramme de Hertzsprung-Russell. Ensuite, en disposant des valeurs de luminosité et en mesurant l’éclat (magnitude apparente) de l’étoile, on peut calculer la distance qui la sépare de celle-ci. Une telle bougie standard donne une idée générale de la distance à la galaxie dans laquelle elle se trouve.

Cependant, cette méthode demande beaucoup de travail et n’est pas très précise. C’est pourquoi il est plus pratique pour les astronomes d’utiliser comme bougies standard des corps cosmiques aux caractéristiques uniques, dont la luminosité est connue au départ.

Bougies standard uniques

Céphéide PTC Puppis

Les céphéides, étoiles pulsantes variables, sont les bougies étalons les plus utilisées. En étudiant les caractéristiques physiques de ces objets, les astronomes ont appris que les céphéides possèdent une caractéristique supplémentaire, la période de pulsation, qui peut être facilement mesurée et qui correspond à une certaine luminosité.

Grâce aux observations, les scientifiques sont en mesure de mesurer l’éclat et la période de pulsation de ces étoiles variables, et donc leur luminosité, ce qui leur permet de calculer leur distance. Trouver une céphéide dans une autre galaxie permet de déterminer la distance de la galaxie elle-même de manière relativement précise et aisée. C’est pourquoi ce type d’étoile est souvent appelé «balise de l’univers»

Bien que la méthode des céphéides soit la plus précise à des distances allant jusqu’à 10 000 000 pc, son erreur peut atteindre 30 %. Pour améliorer la précision, il faudrait disposer du plus grand nombre possible de Céphéides dans la même galaxie, mais même dans ce cas, l’erreur est réduite à au moins 10 %. La raison en est l’imprécision de la relation période-luminosité.

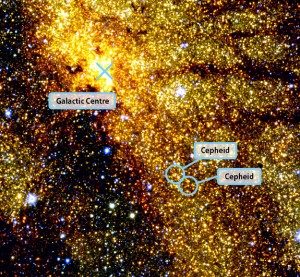
Les céphéides sont les «phares de l’univers».

Outre les céphéides, d’autres étoiles variables dont la relation période-luminosité est connue peuvent être utilisées comme bougies standard, de même que les supernovae dont la luminosité est connue pour les plus grandes distances. La méthode utilisant des géantes rouges comme bougies standard est proche de la méthode des céphéides en termes de précision. Il s’est avéré que les géantes rouges les plus brillantes ont une magnitude stellaire absolue dans un intervalle suffisamment étroit pour permettre le calcul de la luminosité.

Les distances en chiffres

Distances dans le système solaire :

• 1 a.e. de la Terre au Soleil = 500 s.s. ou 8,3 s.min.
• 30 u.a. du Soleil à Neptune = 4,15 heures-lumière.
• 132 a.e. du Soleil — c’est la distance à la sonde Voyager 1, a été observée le 28 juillet 2015. Cet objet est le plus éloigné de ceux conçus par l’homme.

Distances dans la Voie lactée et au-delà :

• 1,3 parsecs (268144 a.u. ou 4,24 années sv) du Soleil à Proxima Centauri, notre étoile la plus proche
• 8 000 parsecs (26 000 années sv.) est la distance entre le Soleil et le centre de la Voie lactée.
• 30 000 parsecs (97 000 années sv.) est le diamètre approximatif de la Voie lactée.
• 770 000 parsecs (2,5 millions d’années sv.) — distance de la grande galaxie la plus proche, la nébuleuse d’Andromède.
• 300 000 000 000 000 pc — l’échelle à laquelle l’Univers est presque homogène
• 4 000 000 000 000 pc (4 gigaparsecs) — la limite de l’Univers observable. C’est la distance parcourue par la lumière enregistrée sur Terre. Aujourd’hui, les objets qui l’ont émise se trouvent à 14 gigaparsecs (45,6 milliards d’années-lumière), compte tenu de l’expansion de l’Univers.

Date de publication: 12-26-2023

Mettre à jour la date: 12-26-2023