Léonard Euler

Leonhard Euler

Enfance et jeunesse

Leonhard Euler est né à Bâle, en Suisse, le 15 avril 1707. La famille vit des modestes revenus de son père, un prédicateur passionné de mathématiques. Il devient le premier professeur du futur scientifique.

Le garçon reçoit son éducation primaire du tuteur du prêtre Johannes Burkhart et, en 1720, il entre à l’université de Bâle pour y poursuivre ses études. Le jeune homme étudie assidûment et fait preuve d’excellentes aptitudes en mathématiques. Ses efforts sont remarqués par l’honorable mathématicien européen Johann Bernoulli et par les érudits de l’Académie russe des sciences, qui l’invitent bientôt à travailler à Saint-Pétersbourg.

Années de travail

En 1727, Leonard s’installe en Russie, rejoint les rangs des membres associés de l’Académie des sciences et, en 1733, occupe un poste au département de mathématiques, où il révèle ses talents uniques. Le scientifique travaille sans relâche sur les fonctions mathématiques, simplifie les opérations analytiques, améliore le calcul intégral et rédige des livres et des manuels pour les universités.

Le bâtiment de l’Académie des sciences de Saint-Pétersbourg. Gravure de M.I.Makhaev.

Un emploi du temps chargé pendant deux ans entraîne la perte de la vision de son œil droit et une détérioration générale de sa santé. Malgré l’abondance de travail, Euler trouve le temps de s’occuper de sa vie personnelle. C’est en Russie qu’il rencontre sa future épouse Katharina Gzell, qui donnera plus tard 13 enfants à son mari.

Le scientifique a dû abandonner son travail en Russie de 1741 à 1766 en raison de la situation politique instable et s’est installé en Allemagne. À Berlin, Leonard travaille sur de nouvelles méthodes de calcul des trajectoires des planètes et de détermination de leur emplacement, permettant de traduire les formules mathématiques en équations plus compactes avec des fonctions incrémentales de valeurs infinitésimales, mais toujours non égales à zéro, au lieu de représentations graphiques et de méthodes descriptives. Cette représentation des mathématiques en astronomie a donné lieu à des études sur la dynamique perturbée de la Lune et d’autres corps cosmiques. De nouvelles méthodes ont permis de décrire le mouvement exact des planètes du système solaire, en tenant compte des interactions entre les corps, de la courbure de l’orbite, de l’inclinaison et de la rotation autour de l’axe.

Contribution à l’astronomie

De retour dans la capitale du nord de la Russie, Leonard développe une cataracte à l’œil gauche, qui prive finalement le scientifique de la vue. Euler avait une mémoire phénoménale et ne réduisait pas l’intensité de son travail, même après avoir perdu la vue. Il a apporté une contribution inestimable au développement des mathématiques, de la mécanique, de l’optique, de l’acoustique et de l’astronomie physique. Le scientifique a accordé une attention particulière au problème non résolu de l’interaction de notre planète avec son satellite naturel, la Lune, et le centre du système, le Soleil. Ses travaux ont servi de base aux tables de calcul de la longitude sur les routes maritimes des navires. Après une longue période de cécité, il continue à développer la théorie des nombres et en déduit la loi de la dépendance quadratique.

Les travaux d’Euler ont servi de base aux tables de calcul de la longitude sur les routes maritimes des navires

Au cours de sa vie, Euler a consacré plus d’une centaine d’ouvrages à l’astronomie, dont l’orientation principale était la mécanique céleste ou «astronomique». La nécessité d’une étude détaillée des problèmes dans cette direction s’est imposée avec le besoin de déterminer la position des navires en état de naviguer, la précision du comptage du temps, ainsi que l’intensité des marées. La question de l’interaction des composants du système solaire et de sa stabilité a constitué une autre raison de mener des recherches sur la dynamique des objets spatiaux. Même Newton a remarqué des déviations dans la vitesse de déplacement des planètes et des satellites, qui avaient un caractère séculaire ou annuel. Euler a établi une classification claire des perturbations et a consacré la majeure partie de sa vie à résoudre ce problème de mécanique astronomique du XVIIIe siècle.

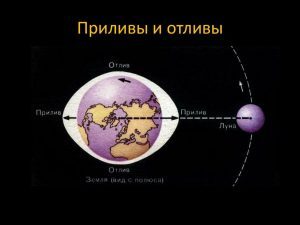
Leonhard Euler a développé une théorie de l’influence de la Lune sur les marées et les régimes de marée.

En 1740, Leonard a développé une théorie de l’influence de la lune sur les marées, pour laquelle il a reçu un prix monétaire de l’Académie des sciences, a justifié le principe du mouvement des comètes et d’autres grands objets sur la base des connaissances de Newton en matière de gravité, a développé une technique connue sous le nom de méthode des quatre ou cinq observations pour déterminer la section conique des comètes, et a formulé une équation pour décrire l’orbite d’une comète. On attribue également à l’astrophysicien la première théorie fondamentale de la «grande inégalité» décrivant le mouvement de Jupiter et de Saturne. Euler a simplifié le calcul exact de la trajectoire de la dynamique des corps perturbés, en appliquant une méthode de calcul approché, appelée plus tard «méthode d’Euler brisée». Un grand nombre de problèmes ont aidé à résoudre la méthode de division des équations linéaires en petites parties constitutives de séquences, où la précision de la détermination de la trajectoire d’un corps céleste augmentait avec la réduction des lignes individuelles et l’augmentation de leur nombre.

Dernières années de sa vie

La tombe d’Euler au cimetière Lazarevsky de la Laure Alexandre Nevsky

Le théoricien améliorait constamment les théories développées, estimant qu’aucune théorie, même la plus élaborée, n’est capable d’exister longtemps sans l’apport de nouvelles données. C’est cette attitude à l’égard de la science qui a permis au scientifique de décrire l’interaction complexe des corps cosmiques de la meilleure façon possible à son époque.

Leonard Euler a quitté la vie le 18 septembre 1783, à l’âge respectable de 76 ans pour l’époque. Le brillant scientifique a continué à travailler jusqu’à ses derniers jours, laissant en héritage des articles qui seront imprimés pendant encore 50 ans après sa mort.

Date de publication: 12-26-2023

Mettre à jour la date: 12-26-2023